Calore specifico

Il calore specifico di una sostanza è definito come la quantità di calore necessaria per innalzare, o diminuire, di un'unità di temperatura una unità di sostanza. A seconda della grandezza fisica scelta per definire l'unità di sostanza, si definiscono differenti grandezze legate al calore specifico. A livello di meccanica statistica o chimica, si sottintende con calore specifico quello numerico o molare (che corrispondono alla stessa grandezza fisica), la grandezza concettualmente più elementare, mentre nelle scienze applicate come l'ingegneria e la termotecnica con calore specifico si sottintende invece il calore massico o volumico che concettualmente derivano dal calore molare. Il calore specifico dipende poi dal tipo di trasformazione in corso.

Grandezze e unità di misura

Calori numerico e molare

Ad esempio il calore specifico può essere definito stabilendo come unità di sostanza una unità di quantità di sostanza, per cui la grandezza individuata prende il nome di calore specifico adimensionale (o numerico o molecolare) o calore specifico molare (o semplicemente calore molare), a seconda che si consideri una molecola (o peso formula) o una mole di sostanza.

Il calore adimensionale, studiato in meccanica statistica, è la grandezza fisicamente più elementare in quanto in base al teorema di equipartizione dell'energia è semplicemente la metà dei gradi di libertà attivi del sistema. Per questo in questo articolo viene indicato semplicemente con c.

In chimica si usa più comunemente misurare il calore molare scegliendo nel Sistema Internazionale l'unità ${\displaystyle \left[\mathrm {J\cdot mol^{-1}\cdot K^{-1}} \right]}$, che si ottiene facilmente moltiplicando il valore adimensionale per la costante dei gas R (circa ${\displaystyle 8,31\,\mathrm {J\cdot mol^{-1}\cdot K^{-1}} }$). Per questo si usa dire in chimica e nelle scienze applicate che l'unità di misura equivalente del calore adimensionale è l'unità R.

Per i gas, la quantità di sostanza può anche essere misurata nelle unità derivate (non SI) normal metro cubo o standard metro cubo (che non sono in effetti unità di misura di volume), e in questo caso il calore specifico viene misurato in ${\displaystyle \left[\mathrm {J\cdot Nm^{-3}\cdot K^{-1}} \right]}$ o in ${\displaystyle \left[\mathrm {J\cdot Sm^{-3}\cdot K^{-1}} \right]}$ moltiplicando per esempio il valore in ${\displaystyle \left[\mathrm {J\cdot mol^{-1}\cdot K^{-1}} \right]}$ rispettivamente per ${\displaystyle 44,618\left[\mathrm {mol\cdot Nm^{-3}} \right]}$ e per ${\displaystyle 42,292\left[\mathrm {mol\cdot Sm^{-3}} \right]}$.

Calori massico e volumico

L'unità di sostanza scelta per definire il calore specifico può però anche essere una unità di massa, e la grandezza corrispondente pertanto viene detto calore specifico massico, o semplicemente calore massico (in questo articolo viene indicato con c^m). L'unità può infine anche essere un volume, e allora si parla di calore volumico (in questo articolo viene indicato con c^v, da non confondere con il calore specifico isocoro c_v).

Per il calore specifico massico l'unità del Sistema Internazionale è il ${\displaystyle \left[\mathrm {J\cdot kg^{-1}\cdot K^{-1}} \right]}$, anche se si usa molto anche la ${\displaystyle \left[\mathrm {kcal\cdot kg^{-1}\cdot {}^{\circ }C^{-1}} \right]}$.

Relazioni fra le grandezze di calore specifico

Il calore massico e quello volumico si ottengono rispettivamente per divisione per la massa molare della sostanza, o per il volume molare della sostanza, quest'ultimo considerato nelle condizioni di pressione e temperatura considerate.

In maniera più astratta, il calore specifico si può definire come il coefficiente tra gli incrementi di temperatura d T e di calore δ Q:

${\displaystyle \delta Q=Nc\ \mathrm {d} T=Mc^{m}\mathrm {d} T=Vc^{v}\mathrm {d} T}$

dove N è la quantità di sostanza e M è la massa della sostanza e V è il suo volume alla pressione e temperatura consuderate, tutte e tre grandezze estensive, legati dalla relazione: N = M/m = V/v in cui m è la massa molecolare media della sostanza (se la quantità di sostanza è misurata in molecole, o massa molare, se la quantità di sostanza è misurata in moli) e v il volume molecolare (o volume molare) della sostanza nelle condizioni di pressione e temperatura considerate. Perciò ne consegue che i calori specifici massico e volumico sono legati al calore specifico adimensionale o molare (la grandezza come si è visto fisicamente più elementare) dalle relazioni:

${\displaystyle c=c^{m}m=c^{v}v}$

Storia

Uno dei primi scienziati a utilizzare il concetto fu Joseph Black, un medico del XVIII secolo e professore di medicina alla Università di Glasgow. Misurò la capacità termica specifica (per unità di massa) di molte sostanze, usando il termine capacità per il calore. Nel 1756 o subito dopo, Black iniziò uno studio approfondito sul calore. Nel 1760 si rese conto che quando due sostanze diverse di uguale massa ma diverse temperature vengono mescolate, le variazioni del numero di gradi nelle due sostanze differiscono, sebbene il calore guadagnato dalla sostanza più fredda e perso da quella più calda sia lo stesso. Black ha raccontato un esperimento condotto da Daniel Gabriel Fahrenheit per conto del medico olandese Herman Boerhaave. Per chiarezza descrisse poi una variante ipotetica, ma realistica dell'esperimento: se si mescolano masse uguali di acqua a 100 °F e mercurio a 150 °F, la temperatura dell'acqua aumenta di 20 °F e la temperatura del mercurio diminuisce di 30 °F (entrambi arrivano a 120 °F), anche se il calore guadagnato dall'acqua e perso dall'acqua il mercurio è lo stesso. Ciò ha chiarito la distinzione tra calore e temperatura. Ha inoltre introdotto il concetto di capacità termica specifica, che è diversa per le diverse sostanze. Black scrisse: “L’argento vivo [mercurio]... ha meno capacità dell’acqua in termini di calore”.

Definizione generalizzata

Esistono svariati modi per esprimere il calore specifico di una sostanza, a seconda dalla trasformazione, e in particolare (notazione) dalla grandezza fisica x conservata nella trasformazione:

${\displaystyle c_{x}=\left({\frac {\partial q}{\partial T}}\right)_{x}}$

in cui q è il calore per unità di quantità di sostanza o di massa e T è la temperatura. Per una trasformazione reversibile, ovvero per un sistema in equilibrio termodinamico, il secondo principio della termodinamica afferma che:

${\displaystyle dq=Tds}$

quindi in questo caso, sostituendo questa espressione del calore, si può ridefinire il calore specifico come:

${\displaystyle c_{x}=T\left({\frac {\partial s}{\partial T}}\right)_{x}}$

Moltiplicando i calori molari per la quantità di sostanza N (o i calori massici per la massa M della sostanza) otteniamo le capacità termiche C_x. In generale si utilizzano due valori, riferiti a una trasformazione a coordinata generalizzata x costante e a forza generalizzata corrispondente F costante:

${\displaystyle {\begin{aligned}&c_{x}=T\left({\frac {\partial s}{\partial T}}\right)_{x}\\[4pt]&c_{F}=T\left({\frac {\partial s}{\partial T}}\right)_{F}\\[4pt]\end{aligned}}}$

Calore specifico isobaro e isocoro

I calori specifici più utilizzati sono riferiti al lavoro di volume: il calore specifico isocoro o a volume costante, reso in simboli come ${\displaystyle c_{V}}$, e il calore specifico isobaro o a pressione costante, ${\displaystyle c_{p}}$ validi per la trasformazione isocora e quella isobara. Se nel sistema i lavori generalizzati sono esclusivamente calore trasmesso e lavoro di volume, allora il primo principio della termodinamica si può esprimere nei potenziali termodinamici: energia interna specifica ed entalpia specifica, equivalenti per trasformata di Legendre:

${\displaystyle {\begin{aligned}&\mathrm {d} u=-p\mathrm {d} v \delta q\\[4pt]&\mathrm {d} h=v\mathrm {d} p \delta q\\[4pt]\end{aligned}}}$

Ricavando il differenziale del calore (che è stato indicato con δ in quanto non è in generale un differenziale esatto):

${\displaystyle {\begin{aligned}&\delta q=\mathrm {d} u p\mathrm {d} v\\[4pt]&\delta q=\mathrm {d} h-v\mathrm {d} p\\[4pt]\end{aligned}}}$

ma a volume costante ${\displaystyle dv=0}$, quindi:

${\displaystyle \delta q_{v}=\mathrm {d} u}$

e a pressione costante ${\displaystyle dp=0}$, quindi:

${\displaystyle \delta q_{p}=\mathrm {d} h}$

quindi dalla definizione di calore specifico a volume costante e a pressione costante:

${\displaystyle c_{v}=\left({\frac {\partial q}{\partial T}}\right)_{v}={\frac {\partial u}{\partial T}}\qquad c_{p}=\left({\frac {\partial q}{\partial T}}\right)_{p}={\frac {\partial h}{\partial T}}}$

altrimenti se ammettiamo anche altre forme di lavoro (lavoro isocoro) nel sistema oltre al lavoro di volume, ovvero altre coordinate generalizzate x_i con ciascuna una corrispondente forza generalizzata F_i,

${\displaystyle {\begin{aligned}&\mathrm {d} u=-p\mathrm {d} v \delta q-\sum _{i}F_{i}\ \delta x_{i}\\[4pt]&\mathrm {d} h=v\mathrm {d} p \delta q-\sum _{i}F_{i}\ \delta x_{i}\\[4pt]\end{aligned}}}$

bisognerà considerare la loro influenza sui calori specifici:

${\displaystyle c_{v}={\frac {\partial u}{\partial T}} \sum _{i}F_{i}\left({\frac {\partial x_{i}}{\partial T}}\right)_{v}\qquad c_{p}={\frac {\partial h}{\partial T}} \sum _{i}F_{i}\left({\frac {\partial x_{i}}{\partial T}}\right)_{p}}$

Sebbene i solidi e i liquidi siano poco dilatabili, la differenza tra ${\displaystyle c_{p}}$ e ${\displaystyle c_{v}}$ non è trascurabile: infatti, per i solidi il coefficiente isoentropico è ${\displaystyle c_{p}/c_{v}\approx 1,05}$ mentre per i liquidi in molti casi è ${\displaystyle c_{p}/c_{v}\approx 1,2}$ ma si hanno anche liquidi con ${\displaystyle c_{p}/c_{v}>1,5}$. Per un aeriforme il calore specifico a pressione costante differisce da quello a volume costante per il lavoro di espansione.

Dipendenza dalla temperatura

Il calore specifico è una grandezza in generale dipendente dalla temperatura. Le correlazioni semiempiriche sono solitamente sviluppate in serie di Taylor fino al quarto ordine:

${\displaystyle c^{0}=a bT cT^{2} dT^{3}}$

con ${\displaystyle c^{0}}$ in ${\displaystyle \left[\mathrm {J\cdot mol^{-1}\cdot K^{-1}} \right]}$ dove a, b, c, d sono tabulate per sostanza e T è la temperatura assoluta. Come si nota dalla figura a fianco, per alcuni gas, in determinati intervalli di temperatura, un tipo di calore specifico può considerarsi costante con essa e questo è particolarmente vero per i gas monoatomici, come i gas nobili.

Relazione di Mayer

Dalla relazione di Maxwell in entropia e temperatura deriva la relazione di Mayer:

${\displaystyle c_{F_{i}}-c_{x_{i}}=T\left({\frac {\partial F_{i}}{\partial T}}\right)_{x_{i}}\left({\frac {\partial x_{i}}{\partial T}}\right)_{F_{i}}}$

Per un sistema termodinamico semplice abbiamo una sola relazione:

${\displaystyle c_{p}-c_{V}=T\left({\frac {\partial p}{\partial T}}\right)_{V}\left({\frac {\partial V}{\partial T}}\right)_{p}}$

Gas perfetto

Nel modello teorico del gas perfetto secondo il teorema di equipartizione dell'energia il calore adimensionale vale:

• Nel caso di gas monoatomici ${\displaystyle {3 \over 2}}$ (isocoro, a volume specifico costante) e ${\displaystyle {5 \over 2}}$ (isobaro, a pressione costante).
• Nel caso di gas biatomici o poliatomici con molecola allineata ${\displaystyle {5 \over 2}}$ (isocoro) e ${\displaystyle {7 \over 2}}$ (isobaro).
• Nel caso di gas poliatomici con molecola non allineata ${\displaystyle {3}}$ (isocoro) e ${\displaystyle {4}}$ (isobaro).

Spesso il gas monoatomico perfetto viene immaginato come uno pseudo-idrogeno, con massa molecolare unitaria m = 1 g/mol.

Per un gas perfetto, che appartiene ai sistemi termodinamici semplici, la relazione di Mayer ha le seguenti espressioni tutte equivalenti tra loro, in ordine dalla più teorica impiegata nella meccanica statistica alla più impiegata nelle scienze applicate:

1. ${\displaystyle c_{p}=c_{v} 1}$
   con ${\displaystyle c_{p}}$ e ${\displaystyle c_{v}}$ i calori specifici adimensionali rispettivamente isobaro e isocoro
2. ${\displaystyle c_{p}=c_{v} R}$
   con ${\displaystyle c_{p}}$ e ${\displaystyle c_{v}}$ i calori specifici molari (si ricordi che per ottenere un calore molare basta moltiplicare il calore adimensionale corrispondente per la costante dei gas R) rispettivamente isobaro e isocoro
3. ${\displaystyle c_{p}^{m}=c_{v}^{m} R^{m}}$
   con ${\displaystyle R'}$ costante specifica del gas considerato, pari a ${\displaystyle R^{m}={R/m}}$ dove m è la massa molare della sostanza, ${\displaystyle c_{p}^{m}}$ e ${\displaystyle c_{v}^{m}}$ i calori specifici per unità di massa rispettivamente isobaro e isocoro (per cui vale ${\displaystyle c_{x}^{m}=c_{x}/m}$)
4. ${\displaystyle C_{p}=C_{V} NR=C_{V} MR^{m}}$
   con ${\displaystyle C_{p}}$ e ${\displaystyle C_{V}}$ le capacità termiche rispettivamente isobara e isocora e N e M sono rispettivamente la quantità e la massa della sostanza.

Determinazione sperimentale

Il teorema di equipartizione dell'energia permette di calcolare agevolmente il calore specifico di un gas con comportamento ideale, su basi di meccanica classica.

La legge di Dulong-Petit stabilisce, su base classica, che il calore adimensionale (o molare) di tutti i solidi è lo stesso, indipendentemente dalla temperatura. IUPAC e IUPAP utilizzano il termine capacità termica specifica o molare, anziché calore specifico e calore molare.

Il calore specifico dipende dalla natura chimica della sostanza considerata e dalla temperatura. Si può ritenere costante solo per piccole variazioni di temperatura e lontano dalle temperature di transizione di fase. Brusche variazioni del calore specifico vengono infatti prese come indice di una transizione di fase solido-liquido, liquido-vapore e anche transizioni cristalline o transizioni strutturali di una molecola.

Anche se per scopi pratici questa definizione è sufficientemente precisa, dal punto di vista teorico essa è solo di un'approssimazione, poiché in realtà il calore specifico dipende dalla temperatura stessa. Per una trattazione più rigorosa ci si può basare sulla capacità termica e definire il calore specifico come la capacità termica per unità di massa.

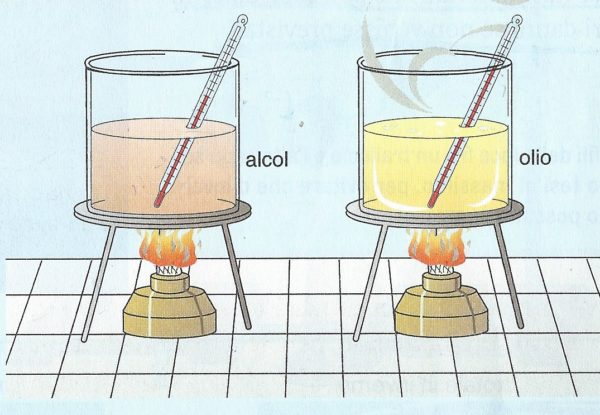
L'acqua a 15 °C ha un calore specifico di 1 cal / (g × °C) mentre quello dell'alcol etilico è di 0,581 cal / (g × °C).

Il calore specifico a pressione e volume costante vengono ricavati rispettivamente a partire dall'entalpia e dall'energia interna, in base alle equazioni:

Per il calore specifico isocoro:

${\displaystyle c_{v}^{m}={\frac {\Delta U}{M(T_{2}-T_{1})}}}$,

dove:

${\displaystyle M}$: è la massa (kg) di fluido coinvolta

${\displaystyle \Delta T=(T_{2}-T_{1})}$: è la variazione di temperatura (K).

${\displaystyle c_{v}^{m}}$: è il calore specifico massico a volume costante.

E per il calore specifico isobaro:

${\displaystyle c_{p}^{m}={\frac {\Delta H}{M(T_{2}-T_{1})}}}$.

Calore specifico isobaro di alcune sostanze

Positività

Premessa: stabilità dell'entropia

Il secondo principio della termodinamica richiede che lo stato di equilibrio termodinamico corrisponda ad un massimo dell’entropia. Questo porta alla conclusione che lo stato è di equilibrio stabile se i vincoli esterni non sono modificati, e questo, a sua volta, significa che la funzione entropia di un sistema semplice è una funzione concava dei parametri estensivi.

Per dimostrare che per un sistema stabile l'entropia è localmente concava, consideriamo due sistemi identici comunicanti tra loro tramite una parete mobile (un pistone) ma isolati dall'esterno da pareti rigide, fisse e adiabatiche. Per simmetria, pressione e temperatura nei due sistemi sono uguali e quindi il sistema è in un equilibrio che è stabile, cioè rimane in equilibrio finché i vincoli non vengono modificati. Tuttavia, se l'entropia S fosse una funzione non concava dell'energia interna U potrebbe avvenire un trasferimento di energia ∆U da un sistema all'altro perché il valore dell'entropia alla fine dello scambio:

${\displaystyle S(U \Delta U,V,N) S(U-\Delta U,V,N)}$

sarebbe maggiore del valore iniziale:

${\displaystyle S(U,V,N) S(U,V,N)}$

Si capisce che questo non avviene per nessun valore dell'energia interna iniziale U. Quindi affinché gli stati di equilibrio siano stabili occorre che l'entropia sia una funzione concava dell'energia, cioè che per qualunque valore di energia interna iniziale U e qualunque suo trasferimento ∆U deve essere soddisfatta la condizione globale di stabilità:

${\displaystyle S(U \Delta U,V,N) S(U-\Delta U,V,N)\leq 2S(U,V,N)}$

Questo implica la seguente condizione locale di stabilità:

${\displaystyle {\frac {\partial ^{2}S}{\partial U^{2}}}\leq 0}$

Questo si estende naturalmente a relazioni fondamentali che includono il volume V e la quantità di sostanza N e più in generale a relazioni fondamentali S=S(X) dove X è un vettore delle variabili di stato di dimensione arbitraria. Le condizioni di stabilità dell'entropia pongono vincoli generali sui coefficienti termodinamici.

Da modelli teorici di meccanica statistica o per estrapolazione dei dati sperimentali è possibile che risultino equazioni di stato che corrispondono a una relazione fondamentale che non soddisfa la concavità dell'entropia in alcuni punti, intervalli o in generale zone (sottodomini) del dominio della funzione di stato entropia, e quindi falliscono nel darebbe descrizione termodinamica corretta in queste zone. È questo il caso ad esempio della legge di van der Waals, che fallisce ad esempio nella campana di vapore saturo. È possibile correggere la relazione fondamentale (e le equazioni di stato corrispondenti) per renderla stabile anche in queste zone (perciò stabile in generale) e quindi anche qui termodinamicamente corretta mediante costruzioni come la costruzione di Maxwell.

Positività del calore specifico

Si è detto nel paragrafo precedente che le condizioni di stabilità dell'entropia pongono vincoli generali sui coefficienti termodinamici. Il calore molare isobaro dipende in effetti dalla derivata seconda dell'entropia dall'energia interna:

${\displaystyle c_{v}={\frac {1}{N}}\left({\frac {\partial U}{\partial T}}\right)_{V,N}=-{\frac {1}{NT^{2}}}\left({\frac {\partial ^{2}S}{\partial U^{2}}}\right)_{V,N}^{-1}}$

La particolare condizione locale di stabilità vista nel paragrafo precedente associata alla dipendenza dell'entropia dall'energia interna:

${\displaystyle {\frac {\partial ^{2}S}{\partial U^{2}}}\leq 0}$

associata con la condizione che la temperatura assoluta è definita non negativa:

${\displaystyle T\geq 0}$

e che naturalmente la quantità di sostanza è definita non negativa, porta quindi naturalmente alla conclusione che il calore specifico è non negativo in un sistema stabile:

${\displaystyle c_{v}\geq 0}$

Calore specifico negativo

Il concetto di "calore specifico negativo", noto implicitamente in astrofisica fin dai lavori di Subrahmanyan Chandrasekhar degli anni 1930, compare in maniera marginale nel classico testo di Fisica Statistica di L.D.Landau ed E.M. Lifshitz, fu diffuso nella comunità dei fisici da Walter Thirring nel 1970. Recentemente ci si è accorti che un qualsiasi sistema con interazioni a lungo raggio (come sistemi autogravitanti, plasmi a una componente) può avere calore specifico negativo. La richiesta più basilare affinché un sistema possa avere calore specifico negativo è che tale sistema non sia additivo. Tranne che per le osservazioni astrofisiche, ad ora non è chiara la verifica sperimentale di tale possibilità.

In altro contesto, all'interno della meccanica statistica di non equilibrio, è stato osservato calore specifico negativo in alcuni sistemi (in particolare in reazioni di multiframmentazione nucleare, nei cluster atomici e in oggetti stellari auto-gravitanti).

Note

Bibliografia

• Paolo Silvestroni, Fondamenti di chimica, 10ª ed., Milano, CEA, 1996, ISBN 88-408-0998-8.
• Giorgio Mazzone, Appunti di termodinamica dei solidi, vol. 1, 1ª ed., Roma, ENEA, 2006, ISBN 88-8286-141-4., cap. 13 Il calore specifico dei solidi, pp. 103–108.
• Sycev, Sistemi termodinamici complessi, Roma, Editori Riuniti, 1985, ISBN 88-359-2883-4., cap. 2, p. 45
• (EN) J.M. Coulson, J.F. Richardson, Chemical Engineering, vol. 6, 3ª ed., Butterworth-Heinemann, 1999, ISBN 0-7506-4142-8.

Voci correlate

• Calore
• Calore latente
• Calore sensibile
• Capacità termica
• Coefficiente di dilatazione adiabatica
• Potenziale termodinamico
• Equazione di Kirchhoff
• Legge di Dulong Petit
• Modello di Debye
• Modello di Einstein
• Relazione di Mayer
• Teorema di equipartizione dell'energia#Calore specifico

Altri progetti

• Wikimedia Commons contiene immagini o altri file su calore specifico

Collegamenti esterni

• (EN) specific heat, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• Calore specifico per alcuni tipi di sostanze, su interfred.it.
• Calori specifici di alcune sostanze, su itchiavari.org.